BST Sequences

A binary search tree was created by traversing through an array from left to right and inserting each element. Given a binary search tree with distinct elements, print all possible arrays that could have led to this tree.

Solution

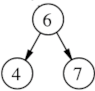
Consider a simple binary search tree with three elements. The root of the tree must have been inserted first - if a different node was inserted first, that node would be the root. After the root has been inserted, the left and right children could have been inserted in any order. The tree below has two possible sequences:{6,4,7} and {6,7,4}.

If we have two sequences which define the order of insert for the left and right subtrees, the set of generalized sequences is defined by all the sequences for which the order of the subsequences is preserved. This can be made more concrete with an example. Let’s say the left subtree was created by the following sequence:

A,B,C

and the right subtree was created by the following sequence:

D,E,F

In order to create the superset of sequences which could have created the entire tree, we need to weave elements from the left sequence with elements from the right sequence. The following are possible sequences which created the two subtrees.

A,B,C,D,E,F
A,B,D,C,E,F
A,D,B,E,C,F
D,A,E,B,F,C
D,E,A,F,B,C
D,E,F,A,B,C

We can write a function which recursively generates the set of possible sequences, given two input sequences. Notice that when building prefix, we cover both cases by removing an element from both sequence_1 and sequence_2. After the weave_lists call returns, we restore both prefix and the sequence to their original state so that we don’t disturb the other calls on the stack.

def weave_lists(sequence_1, sequence_2, results, prefix):
  if(len(sequence_1) == 0) or (len(sequence_2) == 0):
    result = prefix[:]
    result += sequence_1
    result += sequence_2
    results.append(result)
    return

  new_1 = sequence_1.pop(0)
  prefix += new_1
  weave_lists(sequence_1, sequence_2, results, prefix)
  prefix.pop()
  sequence_1.insert(0, new_1)

  new_2 = sequence_2.pop(0)
  prefix += new_2
  weave_lists(sequence_1, sequence_2, results, prefix)
  prefix.pop()
  sequence_2.insert(0, new_2)

Now, we need to build another recursive function which builds the sequences.

def generate_sequences(node):
  results = []

  if(node == None):
    return [[]]

  prefix = [node.key]

  left_sequences = generate_sequences(node.left)
  right_sequences = generate_sequences(node.right)  

  for i in range(len(left_sequences)):
    for j in range(len(right_sequences)):
      weaved = []
      weave_lists(left_sequences[i], right_sequences[j], weaved, prefix)
      results.append(weaved)

  return results