Decision Trees

Insertion sort, merge sort, heap sort and quick sort are all examples of comparison sorts. They sort the elements of a set by making comparisons between elements. The sequence of operations in a comparison sort can be represented as a decision tree, where each node of the tree represents a comparison. The tree below describes a sorting algorithm operating on a set of 3 numbers. Since a set with 3 elements has 6 permutations, there will be 6 leaves on the decision tree.

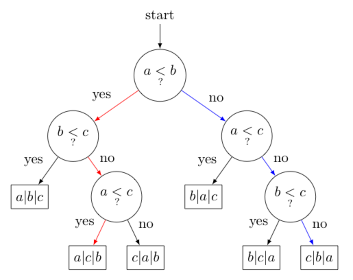
The leaves represent possible outcomes of the sorting process. The longest path from the root of the tree to a leaf represents the maximum number of comparisons - the worst-case scenario for the sorting algorithm. Said differently, the height of the tree represents the worst-case runtime of the algorithm.

Let’s find the maximum height of the decision tree. First, we will assert that a set with \(n\) elements has \(n!\) permutations, and therefore a decision tree which represents a sorting process must have at least \(n!\) leaves. Next, we will note that a binary tree of height \(h\) has a maximum of \(2^h\) leaves.

\[n! \leq 2^h\]

Let’s take a base 2 logarithm of both sides.

\[h \geq \log (n!)\]

Stirling’s approximation allows us to simplify \(n!\).

\[\left( \frac{n}{e} \right)^n < n!\]

Substituting Stirling’s approximation into our equation for \(h\),

\[\\ h \geq \log \left( \frac{n}{e} \right)^n \\ h = n \log n - n \log e \\ h = \Omega (n \log n)\]

Thus, any decision tree which sorts \(n\) elements has a height of \(\Omega (n \log n)\). We will not be able to acheive linear time with a comparison sort algorithm.