Binary Search Trees

A binary search tree is a tree that satisfies the following relationship: each left child is less than or equal to the parent, and each right child is greater than or equal to the parent. Inspect the root node in the binary search tree below, and you will notice that the left child is less than 8, and the right child is greater than 8.

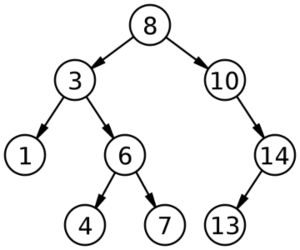
A binary search tree can be represented as a data structure composed of linked nodes. In addition to the key, each noden in a binary search tree will have three attributes : a parent, a left child, and a right child. The children attributes can be null, but the parent attribute must be non-null for all nodes excepting the root node.

class Node:
  def __init__(self, key):
    self.key = key
    self.p = None
    self.left = None
    self.right = None

Insert

To insert an element into the tree, we will need to trace a path downward from the root of the tree. As we make our way down the tree, we will compare the key of the element to nodes in the tree. If the key is greater than the value of a node, we will continue our search with the right child. If the key is less than the node, we will continue with the left child. Notice that the runtime of insert will depend on the height of the tree - in a tree of height \(h\), insert has runtime \(O(h)\).

class BinarySearchTree:
  def __init__(self):
    self.root = None

  def insert(self, key):
    y = None
    x = self.root
    z = Node(key)

    while x is not None:
      y = x

      if(z.key < x.key):
        x = x.left
      else:
        x = x.right

    z.parent = y

    if(y is None):
      self.root = z
    elif(z.key < y.key):
      y.left = z
    else:
      y.right = z

Search

Searching a binary tree can be considered as tracing a path from the root node down the tree until the element in question is found, or the end of the tree is reached. We can build a search method using recursion. The method will compare the key to the current node, and depending on whether the key is greater than or less than the current node, the node will be updated to the left or right child. Note in the code below we need a wrapper method search_tree to call search on the root node.

  def search(self, key, node):
    if node is None:
      return -1
    elif node.key == key:
      return node

    if (key < node.key):
      return self.search(key, node.left)
    else:
      return self.search(key, node.right)

  def search_tree(self, key):
    self.search(key, self.root)

The nodes encountered by the search form a downward path from the root of the tree. In the worst case, this path will be the height of the tree. Thus, the worst-case runtime for search_tree is \(O(h)\) where \(h\) is the height of the tree.

Height

Operations on a binary search tree are dependent on the height of the tree. In the optimal scenario, the binary tree will be complete and the height of the tree will be a minimum. In the worst-case scenario, the binary tree with \(n\) nodes will have a height of \(n\), and will simply be a chain of elements. The average scenario is of course between the best-case and the worst-case scenario.

The height of the binary tree depends on the sequence of the elements which is inserted. Two binary trees containing the same set of elements can have different structures if the elements are inserted in different orders. In our analysis, we can consider a randomly built binary tree, so that each permutation of the set is equally likely.

It can be shown that the average height of a randomly built binary search tree with \(n\) distinct keys is \(O(\log n)\).