Graph Search

Graphs are collections of nodes with edges between them. Trees are a subset of graphs - trees are connected graphs without cycles. The graph below is a directed graph - the edges have directions.

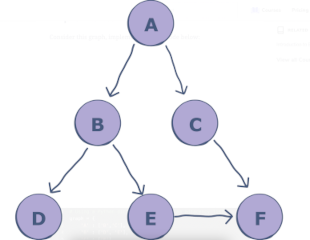
Consider the graph above. One way to represent this graph is as an adjacency list. We can create a list for each node, to represent all the edges departing from that node.

graph = {
    'A' : ['B','C'],
    'B' : ['D', 'E'],
    'C' : ['F'],
    'D' : [],
    'E' : ['F'],
    'F' : []
}

Depth First Search

A depth first search starts at the root, and explores each branch completely before moving on to the next branch. In our algorithm, we will need to keep track of the nodes we have visited so that we do not visit a node more than once.

def depth_first_search(graph, node, visited=set()):
  if(node not in visited):
    print(node)
    visited.add(node)

    for neighbor in graph[node]:
      depth_first_search(graph, neighbor, visited)

The depth-first search will return the following elements for the graph above:

A, B, D, E, F, C

Breadth First Search

A breadth first search starts at the root and explores each neighbor before proceeding to any children. The BFS goes “wide”, while the DFS goes “deep”. The BFS uses a queue to keep track of the nodes it still needs to explore.

def breadth_first_search(graph, node):
  visited = set()
  queue = []

  visited.add(node)
  queue.append(node)

  while(queue):
    s = queue.pop(0)
    print(s)

    for neighbor in graph[s]:
      if(neighbor not in visited):
        visited.add(neighbor)
        queue.append(neighbor)

The breadth-first search will return the following elements for the graph above:

A, B, C, D, E, F